3 STReTCH Module

3.1 Introduction - Statement of objectives

Despite a wide range of development strategies - architectural models sensu (Hallé, Oldeman et al. 1978) - all trees face the same fundamental constraints in terms of light capture and notably need to strike a balance between investment in support structure and assimilatory organs. The objective of the Stretch module is to propose a generic model to represent crown shape flexibility in response to light and space limitations independent of the detailed tree architecture. We believe that a proper crown model should in particular be able to allow for the simulation of a number of “typical” development trajectories. Responses expected to be covered by the new crown model include:

• Flexible growth allocation either towards lateral crown expansion or towards growth in height depending on the prevailing light environment. Ex: a sapling growing slowly (with limited crown development ) in the understorey until a gap occurs in the canopy above it, the successive release in growth (“rush towards the light”) and the subsequent vigorous lateral expansion of the tree crown once the tree has reached the upper canopy (or possibly its death if the canopy gap closes by lateral growth before the tree makes it to the top).
• The model should be able to reproduce the change in crown ratio (crown depth/total tree height) as well as the change in height/dbh allometry coefficients observed for trees under different planting densities.
• The model should also be able to simulate the asymmetric growth resulting from row planting which allows an efficient occupation of space without significant decrease in overall tree growth rate (cf. low sensitivity of rubber dbh increment to planting pattern for a given planting density).

In the Stretch approach the crown is represented by a growing deformable solid. This expanding polyhedron is defined by a set of vectors (later referred to as “Virtual Branches”) all stemming from the crown base. The growth rate of those Virtual Branches (VB) is a function of (local) light conditions (local response) and their relative position (to capture the crown elongation a species specific characteristic). The way in which VBTs are affected by (local) light conditions or constrained by their relative position within the crown is species dependent.

3.2 Ecological basis – Biological Principles

While overall growth - as captured by the dbh increment – will decrease under sub-optimal or supra optimal light levels, crown shape may also be affected by sub-optimal or anisotropic light and in return affect overall growth performance. Two major mechanisms may contribute to crown shape alteration under specific light conditions

A/ Local asymmetric competition between branches within a tree The so-called branch autonomy theory states that the local carbon balance between production and demand for growth and respiration determines the fate of the branch and notably whether it will be shed. However there is increasing evidence that such a simple view is not tenable (Henriksson 2001; Sprugel, Brooks et al. 2002; Lacointe, Deleens et al. 2004). Notably it was shown that the light level at which a branch will be shed depends on the relative light level (to the rest of the crown) rather than the absolute level of light experienced. Even though dominant trees have more resources to allocate, branches on suppressed trees are able to grow and produce new foliage at solar irradiances where branches on dominant trees die. Thus branches are sufficiently interdependent that a positive carbon budget by itself does not ensure branch survival; branch position relative to other branches on the same tree is also important (Sprugel et all, 2002). Furthermore, the increased growth of non-shaded branches in trees where only two branches were shaded suggests that resources were preferentially allocated to branches in more favorable positions (Henriksson 2001). Hence we expect that local deformation of a crown (for example the opportunistic development of a part of the crown in response to local abundance of light (side gap, row planting etc) will be better modeled as a combination of the overall growth potential modulated by local gradients.

B/ A whole tree active shade avoidance response under low light/strong vertical light gradient by which crown growth is reoriented towards height at the expense of lateral growth and which is commonly observed under high tree population density or low light levels. This response may result from a combination of biological mechanisms. Relative or absolute increase of growth in height may also be a response of internal competition of allocation of “growth potential” within the crown as a decreasing gradient of light (or space!) availability from apex to base is common. Hence the distinction made here between global or local response is somewhat arbitrary and is made for operational purposes. Vertical light gradient of increasing intensity towards the top of the canopy is not only common under dense planting where overhead light is abundant while lateral light is very much restricted but also in the forest understory where a similar gradient (though probably less pronounced) may prevail in many cases. Hence new leaves are produced where light resource is most abundant (a local response) which translates into a global deformation of the crown: only the upper-most part of the crown receives adequate light to maintain active growth and therefore elongation of crown occurs. The strategy of "compression" in the understorey and accelerated growth under gap as described in (Sterck 1999) for example would indicate that for canopy species whose juveniles start to grow in the understorey, the relevant signal to trigger accelerated growth in height might be the light gradient rather than the light level… It has been shown that poplar trees can alter their growth rates under modified red/far red ratio and noticeably increase their relative growth in height (Gilbert, Seavers et al. 1995). This may be a widespread response to shading (Ritchie 1997) however our observations do not clearly support the assumption that the overall light level (which is correlated to the red-far red ratio) is associated with enhanced growth in height and this is not implemented in the present model.

3.3 Crown shape modeling

3.3.1 analytical framework

Crown development is decomposed into vertical extension and horizontal extension of VBs (“Virtual Branches”), and light may affect each directional component differently. Growth of an individual VB will depend on

1. Overall growth potential: Individual VB growth will depend on the overall (potential) crown volume increment associated with dbh increment (which notably depends on overall light limitation). The relationship between crown volume increment and dbh increment is controlled by h-dbh power relationship and dbh-CW linear relationship.
2. Species crown profile (default implementation is half ellipsoid): in order to maintain the general shape of crown profile (ellipsoidal, conical, paraboloic of revolution) in the absence of deformation due to competition, the growth of any VB is a function of its relative position in the crown.
3. Vertical stretching resulting from reallocation of growth from lateral expansion to height increase (a response to the light gradient) it is constrained by species specific plasticity (flexi). Vertical stretching of crown is done by co-limiting its lateral extension through associated limitation in dbh increment assuming that total stem biomass scales isometrically with the product of stem cross sectional area and tree height. Crown size is further reduced (shedding lower VBs) via the relationship linking maximum crown volume to dbh established for free growing trees.
   Note that we neglect the possible increased slenderness that may result from overall low light level independently of light gradient. Preliminary experimental data indicate that low light will also tend to increase the h-dbh ratio as well as decrease the crown depth but contrary to crowding it may also increase (slightly as for pulai eg) the crown_width/dbh ratio. However low light level is most probably associated to a significant light gradient in an agroforest stand and we chose not to introduce an additional parameter (governing elongation response as a result of overall low light level) until it can be demonstrated that an effect of light level on elongation of ecologically meaningful amplitude, independent of the light gradient effect exists. A number of casual observations indicate that crown rise is accelerated by increased light gradient (e.g. durian with low branches until it reaches the upper canopy and emerges, shorter rubber trees with reasonable crown depth under dense stand of rubber trees themselves having the crown reduced to the most extreme top of the tree). This would illustrate a change in growth strategy (growth allocation pattern) in response to gap opening for example. In the proposed implementation of the model increased slenderness will force crown rise (see below). In other words the signal that triggers morphological response is the light gradient (vertical light gradient for height growth, anisotropy for crown lateral deformation). We further introduce a species specific sensitivity parameter to capture differing level of responsiveness to light gradient intensity
4. A local deformation factor The impact of local light level (spatial heterogeneity of the incoming light = light anisotropy) is modeled by modulating the horizontal extension as a function of the relative (to average) illumination of light sector associated to each VB. The degree of crown plasticity is assumed to be identical to flexi and is hence species specific. Some additional species-specific parameter might be necessary to refine species differences. This flexibility can be adjusted through the amplitude of the sectoral light used to define the local light level (the larger the sector the lesser the difference in light perceived by neighbouring VBs)

3.3.2 The Algorithm

3.3.2.1 Vertical stretching of crown

Compute vertical and horizontal growth component of VBs of reference tree based on species specific shape and actual overall growth reducers Computation of stem height and dbh increments are described See section 2.3 Height Increment. Those values are then used to compute crown stretch by computing VB increments based on crown profile

3.3.2.2 A/ half ellipsoid profile

(vi_a) VB_incr_ver=cos (theta) * height_inc

(vii_a) VB_inc_hor= sin(theta) * a* dbh_inc

where a refers to the linear relation between dbh and crown width i.e. crown_width = a*dbh + b and theta is the angle of VB with vertical If VB_Tip is inside neighboring crown horizontal component is set to 0 (but height increment is still applied to ensure decent crown profile).

3.3.2.3 B/ Conical profile

Assumptions identical to above (implicit assumption: dbh =dcbh)

To maintain conical profile we compute the expected displacement (absolute increment) of all VBTips as a function of height growth and lateral extension of crown base. Let H be the crown depth length and L the expected (not necessarily equal to actual!) crown radius at crown base for previous dbh (before current time
step increment), then expected VB length of angle q with vertical is

l= (sinq/L + cos q/H)^-1

let L’=L + height increment and H’= expected crown radius at crown base for new
dbh (previous dbh + dbh_inc) then expected new length of VB with
angle q with vertical is

l'=(sin/L' + cos/H')^-1

and the current increment in length of VB of angle q is computed as l’-l

where L= (a*dbh +b)/2

3.3.2.4 Step 2: lateral deformation of crown

Based on the sky map and the light model adjust VB_inc_hor only for anisotropy of incoming light. At this stage we assume that the number of VBs per tree is fixed and set to the following:

default number of VBs on vertical direction is 15 (6 degrees each), and 15 VBs for lateral direction (12 Degrees).

Then the default number of azimuths of the sectoral light map is set to 15 (same as the number of VBs for a given inclination. The number of inclinations of the sectoral light map is set to 5 (equal to number of inclination in the light model, medium precision).

Orientations of VBs is randomized by choosing the first VB randomly.

Number of VBs and sectoral light resolution is not accessible to user

For each of the (15-1) * 15 VB directions (excluding vertical VBt) we compute a index of efficient lighting for each direction and the average value of the index. Note that this is done for all directions (whether there is or not a corresponding VB alive). The ratio of this light level to the average light level is used to adjust the horizontal component of growth for each growing VB. Note that whether there are VBs missing or halted does not affect the deformation of the remaining VBs.
Also note that the growth modifier may theoretically reach values as high as the number of directions! This would happen in case all directions but one have ffective light of zero (completely opaque) in which case the growth modifier for the only growing VB would be equal to the effective light of that particular azimuth/average effective light = number of azimuths. Such extreme cases are however not possible with the default parameterization due to built-in correlation between the levels of light perceived by adjacent VBs (overlapping of sectors). Finally extreme departure from the mean value are only likely to occur when a large majority of VBs perceive very low light levels which is necessarily associated to low CP and low overall growth and hence individual growth of VBs should remain within reasonable boundaries.

Let G(i) be the standard growth rate (equal for all azimuth) computed in previous step
Let L(i) be the sectoral light associated to VBazimuth i
The following algorithm is used to adjust G(i) to L(i).

Step 1
“Effective” light level L’(i) is first computed for each VB direction as
If L(i) > optilum
then L’(i)= optilum
else L’(i)=L(i)

Step2
For all VB present, not halted by collision, and receiving sufficient light (see below shedding step1 for details and notably additional condition that limits the total crown surface that may be lost in one time step through shedding due to low light) G’(i), the modified growth rate is computed as

If L’(i)>AVG(L’(i))
G’(i)=G(i)*(1+flexi* (1-(AVG (L’(i)/L’(i)))^sensi))
IF L’(i)<AVG(L’(i))
G’(i)=Max(G(i)* (1-flexi* (1-(L’(i)/ AVG (L’(i)))^sensi)),0)

The above formulation is consistent with the way flexi and sensi are used to implement response to vertical gradient (flexi essentially a multiplicative factor applied to growth rate, and sensi a index of sensitivity to light gradient either vertical or anisotropic.

Finally if VB is inside neighboring crown (i.e. has intruded a neighbouring crown G’(i) is set to zero (no growth through neighbor's crown envelope)

3.3.2.5 Step 3: branch shedding

Branch shedding always starts with lower most VB in any azimuth.

1/ A first test for VB survival is made prior to VB growth. If VB sectoral light-level is below a certain threshold then it is dropped. Threshold light level at which lower most VBs are shed should be dependent on overall light level (i.e. be relative to overall light level) and more responsive crowns (more flexible, more sensitive) should drop their lower most VBs more rapidly. This is partly covered through step 2 but only for well developed crowns (crown which are severely constrained
by neighbors for lateral extension may never reach surface sizes which allows for step 2 condition to come into play). Hence we make the local light level threshold dependent on relative light level to overall light level.
Practically we compare the perceived local light gradient (L’(i)/AVG(L’(i))^sensi to minilum/AVG(L’(i) and shed branch if perceived light level is below the latter. Equivalent to
If L’(i) < AVG(L’(i)* (minilum/AVG(L’(i))^(1/sensi)
If sensi is above 1 (sensitive species) VBs are shed even if L’(i) is above minilum; conversely if species is not sensitive (sensi below 1) compensation occurs and VBs can be maintained at light levels below minilum. For sensitive species, the stronger the average light level the faster the poorly lit VBs will be shed (mimicking a shade tolerance response by acclimation). Conversely for non sensitive species threshold light level determining shedding decreases with increasing light (there lower most VBs are less sensitive to less than minimum light as more growth can be reallocated to them from better lit branches) . If sensi=1 then threshold light is equal to minilum and independent of AVG(L’(i))
Minilum is the minimum overall light level that allows for growth to occur. AVG(L’(i)) should therefore be above minilum. However this is not necessarily the case as we compute overall light (and subsequent growth) based on the full light model without trimming above optilum. Hence if this happens a specific provision needs to be made. Finally the proposed algorithm is:

If AVG(L’(i))<minilum
then branches are potentially shed if
L’(i)<AVG(L’(i))
else
branches are potentially shed if
L’(i) < AVG(L’(i)*
(minilum/AVG(L’(i))^(1/sensi)
endif

Note that the above formulation does not link branch shedding to reallocation of growth pattern but only to the perceived light gradient (via sensi) and thus is not entirely satisfactory. However sensitivity and flexibility should be correlated (highly sensitive non flexible is a combination that does not make sense). Further more the relative decrease in growth rate is somewhat arbitrarily computed (and trimmed). Sensitive species should deploy a shade avoidance strategy and should correlatively likely have higher minilum, higher flexibility, and (?) lower porosity. In the present form high flexi values (high crown plasticity) seems to confer an advantage in terms of rapid regrowth of crown (compensation growth) as flexibility will likely allow for more than proportional crown surface increment and faster recovery if a gap happens to occur in the vicinity of an otherwise strongly constrained tree for example (provided it is coupled with a high sensitivity to detect the gap…)

2/ Once VB have grown the crown surface is checked against the expected crown surface (cf allometric relation between dbh and crown volume in open grown
trees). In case current crown surface is above reference crown surface additional selective branch shedding will occur until crown surface is reduced to the maximum possible crown surface. VBs are dropped one by one starting with the VB receiving the lowest light (comparing lower most vb along all azimuths).
Algorithm implementation if crown volume is used instead of crown surface as index of crown size: First, each VB is assigned a weight approximating its
contribution to crown volume . The elementary volume associated to a VB used to compute is weight is the volume of the 2 tetrahedra defined by the three vertices defined by the closest 3 neighboring VBs. left, right and top neighbors, and the target VB itself. The weight of a VB is then computed as the sum of the elementary volume assigned to it to the sum of all such elementary volumes. When a particular VB is dropped the total crown volume is reduced proportionally to the weight of the shed VB.

NOTES:

1. Will still need to introduce an interface to allow for a possible systematic crown rise of reference (open grown) tree .
2. NO significant crown overlapping is tolerated in the model except for possible in-growth of a tree within a larger overhanging crown (see below). At present
   a species with low flexibility and high shade tolerance will show higher crown boldness as it will retain its VBs longer and fail to
   reallocate growth preferentially to well lit VBs. Differential "crown shyness" could further be controlled by limiting the number of steps a VB may survive if halted
   growing. As a consequence species tolerant to low light may in fine be even more tolerant to crown collision as they may be halted only temporarily and resume growth once the other crown has shed its branches
3. At each time step VBs are resampled (along a set of fixed directions) and VBTs new position interpolated from previous VBs positions. If VBs are missing, the lower most remaining VB is always located along the vector immediately below (larger angle with vertical) the existing VB at the same distance from tree vertical axis. If all VBs along a particular azimuth have been dropped a new VB is regenerated with length equal to average length of all VBs of same inclination.

3.4 Collision detection

Collision determines halt of growth of VB The collision between neighboring crowns is detected if there is intersection between the horizontal vector joining VBT to tree crown vertical axis and any triangle defined as a result of triangulation of VBTs location in 3D of neighboring tree.

Note that as a result of this implementation vertical growth rate of tree top apex is not affected by collision. However the VB growing from inside another crown will be halted if they come to intersect with containing crown envelope.

3.5 Triangulation algorithm

A proprietary triangulation algorithm is used which takes advantage of the fact that VBs are regularly spread and notably that on a given azimuth there can be
no missing VB between lower most VB and apex.

Let n be the number of azimuth and p the number of inclinations. The total number of VBs (including apex) in a full crown (no missing VB) is then n*(p-1) + 1 and the associated number of triangles is n*(2(p-2) + 1)=n* (2p-3).

Each time a non-vertical VB is dropped, so are two triangles as can be seen from the algorithm below and illustrated in the figures. The algorithm: Let H(i,j) be a VBTs height at inclination index i and azimuth index j. (assuming that each VBTs has height and horizontal distance from axis)
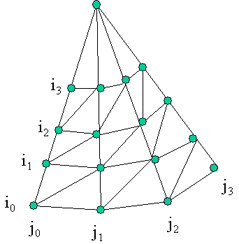
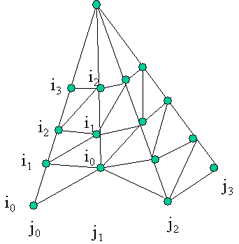
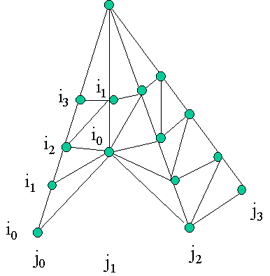
i = 0 is the lowest VBT for each azimuth direction.

The following algorithm iterate the VBTs through the inclination index on the two following series of VBTs per azimuth directions H(Ia, Jc) and H(Ib, Jc+1).

Step a:
For each increments of Ia and Ib, start from a=0 and b=0, find Min(H(i1, Jc), H(i2, Jc+1)) , store the result as one of triangle element. If the lowest VBT is in J series then a++ else b++ (increase one step).

Find next element Min(H(i1, Jc), H(i2, Jc+1)), store it (VBTs with the same index) as the second element of triangle.

Step b:
If the two stored triangle element is on the same series of azimuth then the third element should be the lowest element on opponent series.

Else increase the i of the lowest VBT series and find next Min(H(i1, Jc), H(i2, Jc+1)) as the third element of triangle.

Store the last two elements of the previous triangle as the elements for the next triangle.

If there is more than 1 VBT left in both series then Go to step b.

Else put the last VBT as the third element, and
Repeat from step a for the next j (azimuth direction index; j++)

*the algorithm below is used for triangulation of semi-irregular VBs location
(previous crown type algorithm). And it’s quite robust.

Figure 1. left figure shows the initial VBTs connection (subpart of a crown VBTs), and the right figure show the possible VBTs connection after a VBT shed at i=0 and j=1. the series of VBTs at j1 then re-indexed for i.

Figure 2: if 2 VBTs are shed.

 

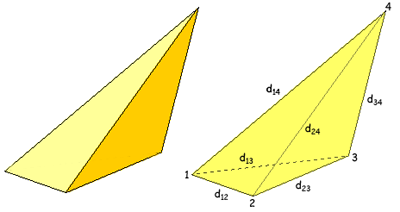
3.6 Algorithm for crown volume computation

Volume of the crown is calculated as the sum of all connected tetrahedra, one face of which is a triangle of the crown envelope (as a result of the triangulation described above). Each triangle is then connected to the center of crown base (added to each triangle as one other vertex to form a tetrahedron).

Then tetrahedron volume is calculated using the formula below: http://mathforum.org/dr.math/faq/formulas/faq.irreg.tetrahedron.html

Let V be the volume of the tetrahedron and d be the distance between vertex. Then

288 V2 =	0	d122	d132	d142	1
	d122	0	d232	d242	1
	d132	d232	0	d342	1
	d142	d242	d342	0	1
	1	1	1	1	0

3.7 Crown deformation and the pipe model theory

We may need to explore further the application of the pipe model in order to link more formally crown volume and dbh values. To maintain consistency between overall crown volume and tree diameter we further assume that leaf area and stem cross sectional area are linearly related. This allometric relationship based on the functional relation between sapwood area and leaf area, is expected to be robust (Morataya, Galloway et al. 1999) and hold under the following provisions

1. Stem diameter is measured just below crown (instead of breast height)
2. Relationship is location specific (under different evaporative demand this relation may be significantly altered)

Then LA is further broken down into crown volume and leaf area density (per unit volume). Assuming LAD to remain stable across time and space within a particular tree this implies that we can extend the allometric relation between stem diameter and LA to stem diameter below crown and crown volume (or crown surface if we consider that leaves are predominantly located on a thin layer on the outer most side of the crown). This relation is used to enforce branch shedding under extreme deformation (elongation) of tree in response to light gradient, i.e. as crown volume is constrained the lower most branches are shed.

A tapering equation could be used to link dbh and diameter below crown so that the assumption of linear relation between stem cross sectional area and leaf area would be more robust. In first approximation a conical truncated shape may be used (based on data collected by Hubert in Krui for example) for the part between diameter at breast height and diameter at crown base height (but see also, for a discussion of the various approaches that may be used, http://sres.anu.edu.au/associated/mensuration/shape.htm#equation). In fact the model should be able to compute cross-sectional area of stem at any height based on any kind of stem profile if such information is provided by user